arctan1=π/4=45°。

计算过程如下

1. arctan表示反三角函数，令y=arctan(1)，则有tany=1。

2.因为 tan(π/4) = 1，因此y=π/4=45°。

arctan 便是反正切的意思，比如：tan45度=1，则arctan1=45度，便是求“逆”的计算，就好比乘法的“逆”计算是除法一样。

不是独特函数值的反正切，需要通过计算器求解。相似的也有arcsin便是反正弦，sin30度=1/2，则arcsin1/2=30度，此外，也有arccos 和arccot 等等。

arctan1等于多少(arctan1=π/4=45°。计算过程如下)

Arctangent（即arctan）指反正切函数，即部分正切函数的 反函数。一般大学高等数学含有涉及。反正切函数是数学术语，指函数y=tanx的反函数。计算方式：设两钝角分别是A，B，则有以下表示：若tanA=1.9/5，则 A=arctan1.9/5。若tanB=5/1.9，则B=arctan5/1.9。假如求具体的视角能够查表或使用计算机计算。

函数y=tanx,（x∈（-π/2,π/2））的 反函数，记作y=arctanx，叫做反正切函数，其定域为R。反正切函数是 反三角函数的一种。一样，因为 正切函数y=tanx在定义域R中不具有一一对应的关系，所以不存在反函数。注意这里选择是正切函数的一个 单调区间。

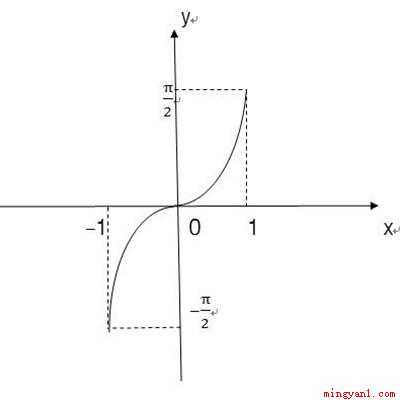
反正切函数的大概图像如图所示，显然与函数y=tanx,（x∈R）关于直线y=x对称，且渐近线为y=π/2和y=-π/2.

tan的每个特殊值，以及arctan的每个特殊值

1.0度角：tan0°=0，arctan0=0°；

2.30度角：tan30°=√3/3，arctan(√3/3)=30°；

3.45度角：tan45°=1，arctan1=45°；

4.60度角：tan60°=√3，arctan√3=60°；

反函数特性

（1）一个函数与它反函数在相应区间上单调性一致

（2）一段连续的函数的单调性在对应区间内具有一致性

（3）反函数是相互的且具有唯一性。

特殊角三角函数值

sin30°=1/2、sin45°=√2/2、sin90°=1，

cos30°=√3/2、cos45°=√2/2、cos90°=0，

tan30°=√3/3、tan45°=1、tan90°不会有。

- END -

阅读剩余 0%
本站所有文章资讯、展示的图片素材等内容均为注册用户上传(部分报媒/平媒内容转载自网络合作媒体)，仅供学习参考。 用户通过本站上传、发布的任何内容的知识产权归属用户或原始著作权人所有。如有侵犯您的版权，请联系我们反馈本站将在三个工作日内改正。